13. Multivariate Gaussian
Multivariate Gaussians
Most robots that we would be interested in modeling are moving in more than one dimension. For instance, a robot on a plane would have an x & y position.
The simple approach to take, would be to have a 1-dimensional Gaussian represent each dimension - one for the x-axis and one for the y-axis.
Do you see any problems with this?
SOLUTION:
There may be correlations between dimensions that we would not be able to model by using independent 1-dimensional Gaussians.The image below depicts a two-dimensional Gaussian distribution.
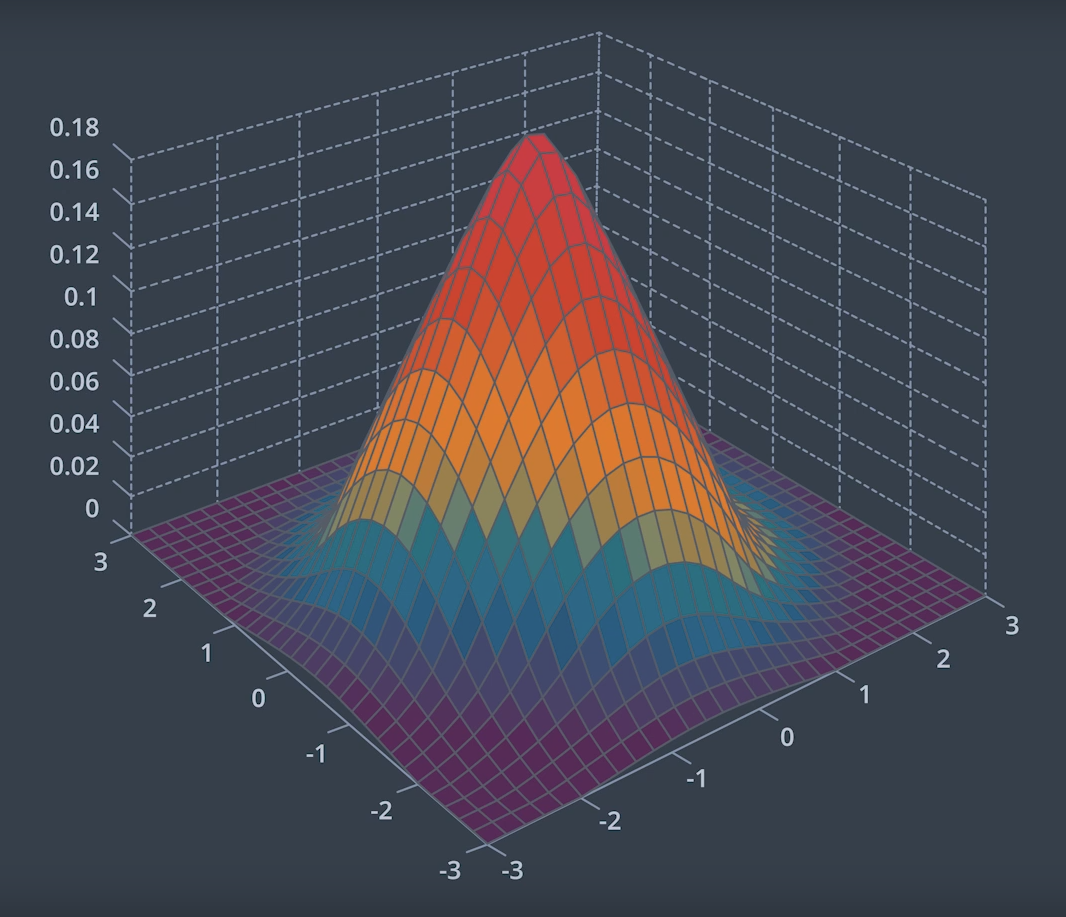
Let's dive into the details!
Multivariate Gaussian
Formulas for the Multivariate Gaussian
Mean
The mean is now a vector,
Covariance
And the multidimensional equivalent of variance is a covariance matrix,
Where \sigma_{x}^2 and \sigma_{y}^2 represent the variances, while \sigma_{y}\sigma_{x} and \sigma_{x}\sigma_{y} are correlation terms. These terms are non-zero if there is a correlation between the variance in one dimension and the variance in another. When that is the case, the Gaussian function looks 'skewed' when looked at from above.
If we were to evaluate this mathematically, the eigenvalues and eigenvectors of the covariance matrix describe the amount and direction of uncertainty.
Multivariate Gaussian
Below is the formula for the multivariate Gaussian. Note that x and \mu are vectors, and \Sigma is a matrix.
If D=1, the formula simplifies to the formula for the one-dimensional Gaussian that you have seen before.